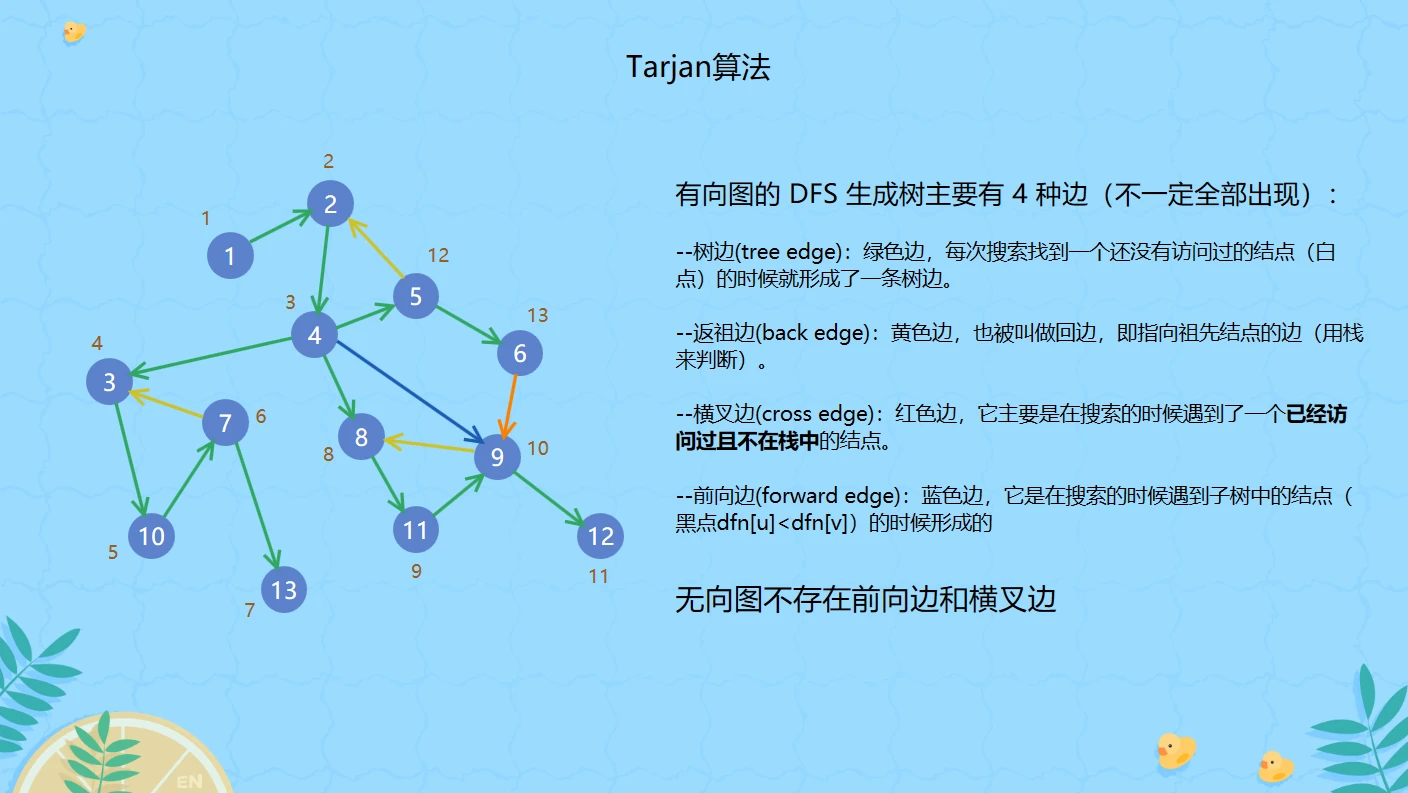
Tarjan算法是由一位名叫Tarjan的人发明的，基于DFS（深度优先搜索）进行缩点操作，将图变为无环图

算法思路

1.首先每个点都对应一个dfn值和low值：

• dfn[u]：记录时间戳，u点是DFS中第几个访问的节点
• low[u]：记录u点不通过父节点能访问到的dfn值最小的点（时间戳最小的点）
• 初始时赋值dfn[u]=low[u]=++time

2.记住树边、返祖边和横插边

• 树边：访问一个没有访问过的点（白点）
• 返祖边：访问到一个已经访问过的点v并且v在栈中
• 横插边：访问到一个已经访问过的点v但v不在栈中

3.详解算法（逻辑部分）

• 从图上某一点u开始，进行DFS(u)，对点u进行dfn[u]=low[u]=++time，赋初值
• 将点u压入栈中，遍历所有u点的邻接边for(int i=head[u];i;i=e[i].next)，将邻接点定义为v点（建议提出来，不然懒得写）int v=e[i].v，此时v点有2种情况：
• 1.dfn[v]==0：即v点没有被访问过，那么就前往v点Tarjan(v)，返回后dfn[v]!=0，更新low值low[u]=min(low[u],low[v])（请画图理解，不要死背！）
• 2.dfn[v]!=0：即v点已被访问过，如果是有向图就要检查是否v在栈中，如果在vis[v]==true，更新low[u]=min(low[u],dfn[v])（请画图理解，不要死背！）
• 3.节点u变黑（计算完所有u的邻接边 / u的子树访问结束），如果dfn[u]==low[u]，那么从栈顶到u为一个环（SCC）